Zagadka forumowa >;) A co to jest? >;))
|
|
No to coś hmm z "zaczarowanego kręgu"
 
|
 
|
|
Było by zabawne jak by ludzie wiedzieli kim, jest hrabia >;)) tzn był bo tytuły zostały zlikwidowane, a kiedy? >;))
 W Polsce przedrozbiorowej tytuł hrabiowski, jak i pozostałe tytuły arystokratyczne były z reguły zakazane jako sprzeciwiające się naczelnej zasadzie równości szlacheckiej. Król Polski mógł jednak mianować hrabiów i z tego przywileju korzystał, ale czynił to wyłącznie w stosunku do Włochów i arystokratów państw obcych, także po unii polsko-litewskiej dla ruskich i litewskich kniaziów jako potomków panujących dynastii. Król Zygmunt August ustanawiał w ten sposób hrabstwa na Szkłowie, Myszy, Bychowie i Hłuńsku (Hłusko Dąbrowickie) będących dobrami Chodkiewiczów oraz na Skumiłowie[potrzebny przypis] (Łohojsku i Berdyczowie[3]) Tyszkiewiczów. Polscy magnaci przyjmowali jednak chętnie, wbrew prawu, tytuły od zagranicznych monarchów. Habsburgowie jako cesarze rzymscy za usługi polskich posłów i dyplomatów oraz niektórym rodom polskim (jak Górkowie, Tarnowscy), nadawali w dowód wdzięczności swoje tytuły hrabiów i książąt Sacri Imperii Romani. Tym sposobem w roku 1473 nadano ten tytuł Leszczyńskim, następnie rodom Górków, Kmitom z Wiśnicza, Lubomirskim, Tęczyńskim w roku 1527, Tarnowskim, Chodkiewiczom i Szydłowieckim. Przedstawicieli tych rodów nazywano po tym „hrabiami cesarstwa rzymskiego”. Do rozbiorów Polski tytuły hrabiowskie otrzymali jeszcze Hyzopscy, Wielopolscy, Przerębscy, Miączyńscy, Koniecpolscy, Radziejowscy i wielu innych. Bez nominacji cesarskiej tytułami hrabiowskimi podpisywali się jeszcze Sapiehowie, Ostrogscy, Sieniawscy i inni, przyjmując tytuł od dóbr własnych. Wartość prawna takich nadań była raczej znikoma. W związku z misjami dyplomatycznymi dla podniesienia prestiżu i rangi delegacji kanclerze królewscy pozwalali wysyłanym posłom na podpisywanie się tytułem hrabiowskim zamiast mało znanego polskiego tytułu komesa. Tuż przed upadkiem Rzeczypospolitej Sejm zaczął również nadawać wbrew tradycji tytuły, m.in. Poniatowskim i Ponińskim. W okresie rozbiorów monarchie obce również nadawały tytuły. We wszystkich zaborach prawo do uzyskania tytułu hrabiego miała rodzina mogąca wykazać się pochodzeniem od senatora Rzeczypospolitej lub osoby piastującej wysokie urzędy koronne. Rodziny pochodzące od urzędników ziemskich lub powiatowych otrzymywały tytuł barona. W Polsce konstytucja marcowa w 1921 pozbawiła tytuły arystokratyczne znaczenia prawnego. W Polsce szyk „imię-tytuł-nazwisko” był zwyczajem jeszcze przedrozbiorowym, jednak ograniczonym do ceremonialnych uroczystości, podpisów itp. Wskutek snobizmu czy też mody konstrukcję tę zaczęto naśladować i stosować szerzej także w języku polskim; stąd czasem zamiast mówić „hrabia Wojciech Dzieduszycki” używa się dość pretensjonalnej w codziennych sytuacjach lub w zwykłym tekście formy „Wojciech hr. Dzieduszycki” czy też „Adam Karol książę Czartoryski”. Osobny artykuł: lista polskich rodów hrabiowskich. Wicehrabia Bezpośrednio niższym tytułem od hrabiego jest wicehrabia (niem. Vizegraf, ang. viscount, fran. vicomte) |
|
Administrator
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
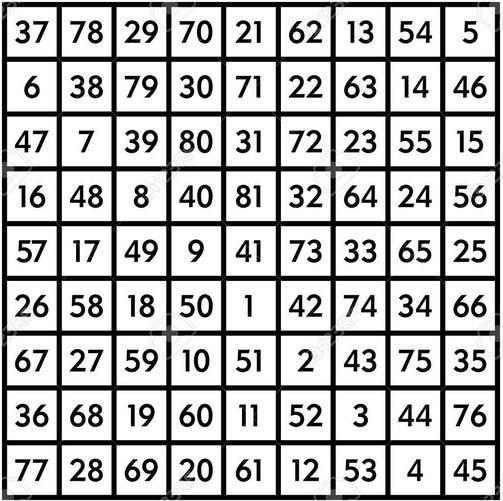
To jakaś magiczna tabelka. Zadałam sobie trud i przeliczyłam te liczby (dodałam do siebie) i w każdym rzędzie wyszło mi 369 Czy to w pionie, czy w poziomie. 
|
|
Administrator
|
Po przekątnej od 37 do 45 też suma jest 369

|
|
Administrator
|
Z prawa do lewa od 5 do 77 suma też równa się 369.
3, 6 i 9 to jakieś magiczne liczby, o których wspominał Tesla... 
|
|
Administrator
|
Jest taka tabelka z tabliczką mnożenia, dla tych, co to nie potrafią na pamięć ;))

|
|
Administrator
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
Zakaz wyprzedzania 

|
|
Brawo Serenko >;) A jako pierwszy był..... kwadrat magiczny 9 podobnież ulubiony pana Tesli >;))
Znak drogowy B-25 zakaz wyprzedzania :) |
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Sylwia
I jeszcze na krzyż to kwadrat magiczny >;) Kwadrat magiczny – kwadratowa tablica (macierz), w której komórki wpisano liczby w ten sposób, że ich suma w każdym wierszu, w każdej kolumnie i w każdej przekątnej jest taka sama[1] (tzw. suma magiczna). Czasem dodatkowo wymaga się, by elementy kwadratu magicznego nie powtarzały się i były dodatnimi liczbami naturalnymi[potrzebny przypis]. Kwadrat, w którym suma liczb w każdym wierszu i każdej kolumnie jest taka sama, ale sumy liczb w przekątnych są różne, nazywa się półmagicznym. Kwadraty magiczne nie mają żadnego zastosowania naukowego, ich układanie jest rodzajem rozrywki matematycznej. Kwadratów magicznych jest nieskończenie wiele. Najpopularniejsze są kwadraty zbudowane z kolejnych wyrazów ciągu arytmetycznego: 1, 2, ... n². Suma magiczna takiego kwadratu wynosi S = n ( n 2 + 1 ) 2 . {\displaystyle S={\tfrac {n(n^{2}+1)}{2}}.} Sposób zrobienia kwadratu 3x3 a-b a+b-c a+c a+b+c a a-b-c a-c a-b+c a+b W tabeli pokazano, jak zrobić kwadrat magiczny 3x3. Wystarczy wybrać jakiekolwiek liczby naturalne dodatnie dla a, b i c, takie, że b/c<>1/2,1,2 oraz a>b+c. Na przykład jeśli a=5, b=3, natomiast c=1, otrzymamy kwadrat jak na rysunku powyżej. Kwadrat magiczny 5x5 23 6 19 2 15 4 12 25 8 16 10 18 1 14 22 11 24 7 20 3 17 5 13 21 9 Na pokazanym kwadracie wpisano liczby od 1 do 25 i ten kwadrat ma następujące własności: każdy rząd daje w sumie 65 każda kolumna daje w sumie 65 każda przekątna daje w sumie 65 każdy 5-liczbowy plus „+” daje w sumie 65 każdy 5-liczbowy krzyżyk „x” daje w sumie 65 duży plus „+” (cztery środkowe liczby na bokach i liczba środkowa kwadratu) daje w sumie 65 duży krzyżyk „x” (cztery liczby na rogach i liczba środkowa kwadratu) daje w sumie 65 gdyby np. przesunąć lewą kolumnę do prawego boku, powstałoby więcej krzyżyków i plusów oraz nowe przekątne, które także dałyby w sumie 65. Jak zrobić kwadrat 5x5 Najprostszą metodą na zrobienie takiego kwadratu jest wpisanie najmniejszej z liczb na środku. W przypadku sumy liczb równej 0 jest to -12. Następnie należy wpisać liczbę o 1 większą w pole znajdujące się o 2 w górę i 1 w prawo (tak jak skoczek porusza się w szachach). W przypadku gdy jest to pole poza kwadratem należy: liczyć od dołu (jeśli za wysoko) lub od lewej (jeśli za bardzo na prawo). UWAGA: przy wpisaniu piątej liczby zamiast poruszyć się „metodą skoczka” powinno się ruszyć o 1 pole w dół! Należy kontynuować zgodnie z „metodą skoczka” do wpisania dziesiątej liczby (znowu ruch w dół) itd. W przypadku sumy liczb równej 5 najmniejszą liczbą jest -11 i dalej powinno się poruszać zgodnie z instrukcjami opisanymi powyżej. W przypadku sumy równej 10 najmniejszą liczbą jest -10 i dalej powinno się poruszać zgodnie z instrukcjami opisanymi powyżej itd. Pozostaje jednak pytanie: co zrobić jeśli suma ma być niepodzielna przez 5? Odpowiedź jest prosta. Należy znaleźć największą liczbę podzielną przez 5 mniejszą od danej liczby i wykonać polecenia do tej liczby. Dalej powinno się odjąć od wybranej liczby liczbę, do której wykonywało się polecenia. Następnie trzeba znaleźć pięć największych liczb i powiększyć je o otrzymaną różnicę. Własności Niektóre własności kwadratów magicznych (n, jak wyżej, oznacza liczbę kolumn i wierszy kwadratu): Jeśli do każdej liczby w kwadracie dodamy tę samą wartość k, to kwadrat pozostanie magicznym, a jego suma magiczna wzrośnie o n·k. Jeśli każdą liczbę w kwadracie pomnożymy przez tę samą wartość k, to kwadrat pozostanie magicznym, a jego suma wzrośnie k-krotnie. Jeśli weźmiemy dwa kwadraty magiczne o tym samym rozmiarze i sumach magicznych S1 i S2, i dodamy liczby na odpowiadających sobie pozycjach, to otrzymany w wyniku tego dodawania nowy kwadrat, który też może być magiczny (nie ma jednak gwarancji, że w tym nowym kwadracie wszystkie liczby będą różne), a jego suma magiczna wyniesie S1+S2. Dla kwadratów trzeciego stopnia (n=3) prawdziwe są też następujące własności: Sumę magiczną kwadratu można szybko wyznaczyć, bez potrzeby sumowania liczb w kolumnach, wierszach bądź przekątnych, za pomocą wzoru S = 3 ( X + Y ) 2 , {\displaystyle S={\tfrac {3(X+Y)}{2}},} gdzie: X – pierwsza liczba kwadratu magicznego (w lewym górnym rogu), Y – ostatnia liczba kwadratu (w prawym dolnym rogu). Wzór ten można zastosować nie tylko do liczb znajdujących się na tych rogach, a do dowolnych dwóch liczb ułożonych symetrycznie względem środka kwadratu. Dodatkowo liczba znajdująca się na środkowym polu kwadratu jest równa 1/3 sumy magicznej. Kwadraty magiczne znali już starożytni Chińczycy[1] i Hindusi, wierzyli w ich magiczną moc i dlatego umieszczali je na amuletach i talizmanach. Chiński kwadrat magiczny, luoshu, miał zostać wynaleziony około 2800 p.n.e. przez Fuxi i dał podwaliny sztuce feng shui. Chińscy architekci radzili stosować magiczny kwadrat podczas projektowania domów, pałaców i miast. Najbardziej znaną budowlą, gdzie podczas projektowania ściśle zastosowano zasadę idealnego kwadratu jest Cesarski Pałac w Pekinie. Przykłady Miedzioryt Melancholia Najsłynniejszym kwadratem magicznym jest prawdopodobnie ten, który umieścił Albrecht Dürer na swoim miedziorycie Melancholia I. Zapewne nieprzypadkowo w dwóch wewnętrznych kratkach ostatniego wiersza tego kwadratu stoją obok siebie liczby 15 i 14, składające się na datę powstania grafiki – rok 1514[1]. [ 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 ] {\displaystyle {\begin{bmatrix}16&3&2&13\\5&10&11&8\\9&6&7&12\\4&15&14&1\\\end{bmatrix}}} Kwadrat z Melancholii Dürera nad skrzydłem anioła n = 4, S = 34 (16+1=17; 10+7=17; 13+4=17; 6+11=17; 15+2=17; 14+3=17; 12+5=17; 8+9=17) Inne przykłady: [ 8 1 6 3 5 7 4 9 2 ] {\displaystyle {\begin{bmatrix}8&1&6\\3&5&7\\4&9&2\\\end{bmatrix}}} [ 1 35 34 4 32 6 7 29 8 30 31 5 33 3 2 36 ] {\displaystyle {\begin{bmatrix}1&35&34&4\\32&6&7&29\\8&30&31&5\\33&3&2&36\\\end{bmatrix}}} [ 37 48 59 70 81 2 13 24 35 36 38 49 60 71 73 3 14 25 26 28 39 50 61 72 74 4 15 16 27 29 40 51 62 64 75 5 6 17 19 30 41 52 63 65 76 77 7 18 20 31 42 53 55 66 67 78 8 10 21 32 43 54 56 57 68 79 9 11 22 33 44 46 47 58 69 80 1 12 23 34 45 ] {\displaystyle {\begin{bmatrix}37&48&59&70&81&2&13&24&35\\36&38&49&60&71&73&3&14&25\\26&28&39&50&61&72&74&4&15\\16&27&29&40&51&62&64&75&5\\6&17&19&30&41&52&63&65&76\\77&7&18&20&31&42&53&55&66\\67&78&8&10&21&32&43&54&56\\57&68&79&9&11&22&33&44&46\\47&58&69&80&1&12&23&34&45\end{bmatrix}}} n = 3, S = 15 n = 4, S = 74 n = 9, S = 369 Zobacz też Zobacz multimedia związane z tematem: Kwadrat magiczny (matematyka) dodekafonia kwadrat magiczny w krzyżówkach kwadrat łaciński kwadrat grecko-łaciński |
|
Administrator
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
Czyli, że co? Tesla to wymyślił? Szłam dobrym tropem? Ps. Trudniejsza zagadka byłaby, gdyby trzeba było w paru miejscach wstawić samemu cyfry ;)) Ojj, na takiej dużej tabeli, gdybym nie znała wyniku, że ma być 369 to pewnie miałabym trudności 

|
|
Administrator
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
Aaa, czyli to nie o Teslę chodzi ;)) Przedobrzyłam :D 
|
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Sylwia
To 369 to zagadka pana Tesli podobnież świat to wibracja, a kto zrozumie będzie rządził światem
 No to jak już będziesz rządzić światem No to jak już będziesz rządzić światem  to.... aż jestem ciekawy co zrobisz? >;P to.... aż jestem ciekawy co zrobisz? >;P
|
|
Administrator
|
 Ktoś zdaje się z tego forum (nie będę pokazywać palcem Ktoś zdaje się z tego forum (nie będę pokazywać palcem  ) ostrzegł mnie, by uważać, czego się pragnie ;) ) ostrzegł mnie, by uważać, czego się pragnie ;)
A u Tesli jest o pragnieniach właśnie. I to jest ten cały sekret! Sorry, ale miałam telefon od siostry... A teraz to już spać muszę  Dobranoc :) 
|
|
Dobranoc Sarenko...Dobranoc Duszki.
|
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Sylwia
Dobranoc, Serenko >;)) A 369?

|
«
Wróć do Magiczna Kawiarenka
|
1 przeglądaj|%1 wyświetleń
| Free forum by Nabble | Edit this page |


