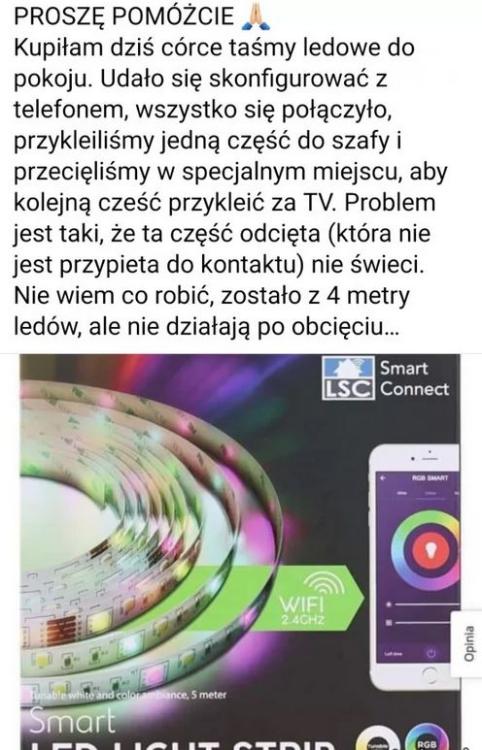
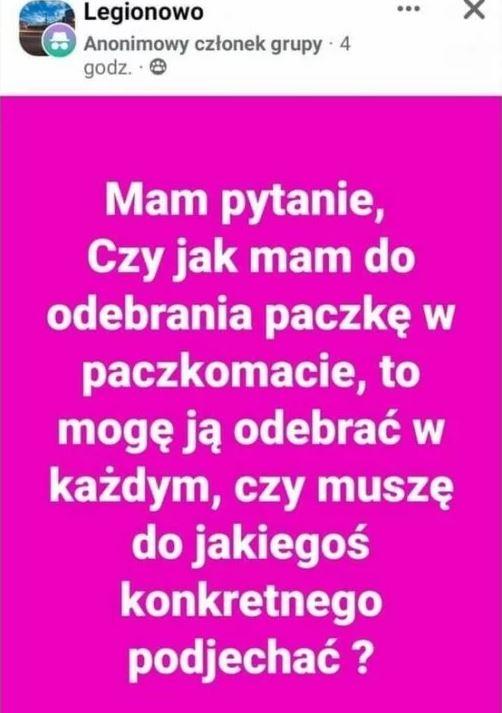
Szykuje się, poważna rozmowa? >;))
12

12

|
|
|
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
A logika?
 Logika (gr. λόγος, logos – rozum, słowo, myśl) – nauka formalna o jasnym i ścisłym formułowaniu myśli, o regułach poprawnego rozumowania i uzasadniania twierdzeń. Historycznie była uznawana za dział filozofii bliski retoryce[1], jednak narodziny rachunku zdań w XIX wieku zapoczątkowały logikę matematyczną. W tradycji zachodniej prekursorem systematycznej logiki był Arystoteles[2][3]. Współczesna logika, wykorzystując metodę formalną, znacznie rozszerzyła pole badań, włączając w to badania nad matematyką (metamatematyka), konstruowanie nowych systemów logicznych (np. logiki wielowartościowe), czysto teoretyczne badania o matematycznym charakterze (np. teoria modeli), zastosowania logiki w informatyce i sztucznej inteligencji (logic for computer science)[4]. Logika klasyczna Formalny system logiczny złożony z klasycznego rachunku zdań i rachunku kwantyfikatorów, zwany też logiką elementarną lub klasycznym rachunkiem logicznym. Przedmiotem tego rachunku są zdania logiczne, to znaczy takie zdania oznajmujące, którym można przypisać jedną z dwu wartości logicznych: prawda lub fałsz. Logika klasyczna jest w tym sensie dwuwartościowa, w odróżnieniu od sformułowanych w XX wieku systemów logik wielowartościowych. W rachunku zdań zdania reprezentowane są przez zmienne zdaniowe (zwyczajowo są to litery: p, q, r, ...). Przy użyciu spójników logicznych, jak „i”, „lub”, „nieprawda, że” (zapisywanych symbolicznie znakami: ∧, ∨, ¬ lub ~[a]) konstruuje się zdania złożone. Jednym z głównych celów rachunku zdań jest wypracowanie metod wyznaczania wartości logicznej zdania złożonego na podstawie wartości logicznych zdań składowych. Szczególnym celem jest opisanie takich schematów zdań złożonych, które są prawdziwe przy każdym podstawieniu dowolnych zdań logicznych za zmienne. Schematy takie nazywane są prawami rachunku zdań. W rachunku kwantyfikatorów zdania złożone budowane są przy użyciu symboli predykatów, zmiennych i kwantyfikatorów – dlatego używa się też nazwy rachunek predykatów. Głównym celem jest opisanie wszystkich schematów zdań z kwantyfikatorami zawsze prawdziwych, czyli praw rachunku kwantyfikatorów. Razem z prawami rachunku zdań tworzą one prawa logiki klasycznej. Każdemu prawu logiki odpowiada schemat niezawodnego wnioskowania dedukcyjnego. Mówi się więc również, że głównym celem logiki klasycznej jest opisanie wszystkich schematów niezawodnego wnioskowania. Klasyczny rachunek logiczny obejmuje wszystkie podstawowe prawa odkryte przez logików starożytnych oraz bardziej współczesne prawa dotyczące kwantyfikatorów. Rachunek ten wystarcza do opisu wszystkich wnioskowań stosowanych w matematyce oraz wszelkich wnioskowań dedukcyjnych[5], i w tym sensie stanowi zamknięty dział logiki. Logika klasyczna jest podstawą wykładu logiki w podręcznikach szkolnych i akademickich. Logika filozoficzna Logika filozoficzna to nauka normatywna, analizująca źródła poznania pod względem prawomocności czynności poznawczych z nimi związanych. Zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Logika, jako dyscyplina normatywna, nie tylko opisuje jak faktycznie przebiegają rozumowania, ale także formułuje twierdzenia normatywne, mówiące o tym, jak rozumowania powinny przebiegać[6]. Pod nazwą logika filozoficzna rozumie się dział filozofii zajmujący się: filozoficznymi problemami logiki (filozofią logiki) zastosowaniem logiki do zagadnień filozoficznych (logiką filozofii) zagadnieniami filozofii języka Logika matematyczna Logika matematyczna (zwana też metamatematyką) to dział matematyki, który wyodrębnił się jako samodzielna dziedzina na przełomie XIX i XX wieku, wraz z dążeniem do dogłębnego zbadania podstaw matematyki. Jej przedmiotem są formalne teorie matematyczne i ich modele, dowody oraz zasięg matematycznych rozumowań. W badaniach stosuje się wyłącznie ścisłe i formalne metody matematyki. Do największych osiągnięć logiki matematycznej należą prace wielu logików i matematyków mające na celu pełną formalizację matematyki, zwieńczone słynnym twierdzeniem Gödla o niezupełności. Twórcami logiki matematycznej byli m.in. George Boole, Gottlob Frege, David Hilbert i Bertrand Russell, a do jej rozwoju przyczynili się między innymi: Jan Łukasiewicz, Alonzo Church, Kurt Gödel i Alfred Tarski[b][4]. Logika w informatyce Formalny charakter logiki współczesnej sprawił, że nie tylko przyczyniła się ona w znacznym stopniu do rozwoju techniki komputerowej, ale też pewne jej działy rozwijają się obecnie w ramach informatyki teoretycznej. Do zagadnień informatycznych o logicznym charakterze należą: systemy przepisywania (rewriting systems), teoria typów, weryfikacja programów (logiki dynamiczne), różne aspekty złożoności obliczeniowej, sieci przełączające (funkcje boolowskie), formalna semantyka języków programowania, programowanie logiczne. Szczególny charakter ma próba zastosowania osiągnięć logiki formalnej w sztucznej inteligencji. Próba ta nie zakończyła się jeszcze wyraźnym sukcesem[5]. Do częściowych sukcesów można zaliczyć praktyczne osiągnięcia w zakresie automatycznego dowodzenia twierdzeń oraz systemów ekspertowych. Zobacz też historia logiki logika intuicjonistyczna logika modalna logika prawnicza logika rozmyta logika wielowartościowa logika wolna analiza logiczna logizowanie Uwagi Istnieją też inne sposoby oznaczania spójników logicznych. Klasyczna monografia podaje, że Polska w proporcji do liczby ludności wniosła największy wkład w rozwój logiki[7]. Przypisy Tadeusz Kotarbiński, Wykłady z dziejów logiki, wyd. 2, Państwowe Wydawnictwo Naukowe, Warszawa 1985. history of logic, [w:] Encyclopædia Britannica [online] [dostęp 2018-01-27] (ang.). Louis F. Groarke: Aristotle: Logic. Internet Encyclopedia of Philosophy. [dostęp 2018-06-27]. (ang.). Witold Marciszewski (red.): Logika formalna: Zarys encyklopedyczny z zastosowaniem do informatyki i lingwistyki, PWN, Warszawa 1987. Andrzej Kisielewicz: Sztuczna inteligencja i logika, WNT Warszawa 2011. Kazimierz Ajdukiewicz: Logika pragmatyczna, PWN, Warszawa 1965. A.A. Fraenkel, J. Bar-Hillel, A. Levy A: Foundations of set theory. Amsterdam: North Holland Publishing Company, 1973, s. 200 |

|
|
Domini Canes.

|
 
|
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
Pewien człowiek zaprosił gości na obiad. Tak się złożyło, że kucharz przy-
palił znaczną część pieczeni. Kiedy gospodarz dzielił mięso na porcje, goście otrzymali mięso nieprzypalone, a członkowie rodziny przypalone. Teraz porównaj to sobie z twoim pytaniem. To prawda, mój przyjacielu, że ludzie pobożni przeważnie żenią się z brzydkimi kobietami. Wiekuisty stworzył w swej mądrości zarówno ładne, jak brzydkie kobiety. Ładne, rzecz jasna, nie będą miały trudności ze znalezieniem sobie mężów. A brzydkie, kto je weźmie? One, jak ta przypalona pieczeń, przeznaczone są dla pobożnych i uczonych w piśmie, którzy należą przecież do bliskich Pana Boga >;P |
|
Nauczyciel:
– Powiedz mi Moryc: jak wygląda gęś? – Gęś? Gęś wygląda oczami… |
|
A co robią wasi rodzice przed zaśnięciem?
Mały Abramek podnosi rękę do góry i powiada: – Ksiądz wie o tym i ja wiem o tym… Ale czy to jest pytanie dla uczniów szkoły podstawowej? |
|
– Szymon, co wiesz o dzieciństwie Mojżesza, wielkiego proroka?
– Mojżesz był synem egipskiej księżniczki… – Źle – przerywa uczniowi nauczyciel. – Córka faraona znalazła go w skrzy- neczce płynącej po rzece… – To tylko ona tak twierdziła, panie profesorze – powiada znający życie uczeń. |
|
Na lekcji religii nauczyciel pyta uczniów:
– Kto mi powie, jaki grzech popełnili bracia Józefa, sprzedając go? Dawidek zgłasza się do odpowiedzi: – Oni sprzedali za tanio i bez opakowania 
|
|
Icek wrócił niedawno z kursu związkowego, na którym bardzo dużo mó-
wiono o materializmie dialektycznym i historycznym. Co to jest materializm dialektyczny trochę zrozumiał, ale co to jest materializm historyczny nie mógł zrozumieć. Przychodzi więc do rabina i pyta: – Rebe, ty jesteś bardzo mądry człowiek, tyle się uczyłeś, powiedz mi, co to jest materializm historyczny? Rebe mówi mu: – Dwóch Żydków w szabas poszło czyścić komin, jeden był brudny, a jeden czysty, który z nich poszedł się umyć? Icek mówi: – Oj, rebe, który z Żydków w szabas będzie czyścić komin? – Jesteś głupi, Icek. Idź do domu, pomyśl i przyjdź do mnie za tydzień. Icek poszedł do domu, intensywnie myślał i znów po tygodniu przyszedł do rebego. Rebe ponownie zadaje mu to samo pytanie: – Chyba ten poszedł się umyć, co był brudny? – Oj, Icek, jaki ty głupi, idź do domu i myśl; za tydzień znów przyjdź do mnie. Icek po tygodniu przychodzi do rebego, a ten mu znowu zadaje to samo py- tanie. Icek zdenerwowany mówi: – Oj, rebe, mnie się zdaje, że ty coś kręcisz. – A widzisz, Icek – mówi mu rebe. – Już myślisz, już wiesz, o co tu chodzi 
|
|
W odpowiedzi na pojawiła się wiadomość opublikowana przez Lothar.
Wojtek,ludzie nie kierują się logika tylko emocjami;)) Nawet jakbys przez tysiąclecia logiki nauczał to przyjdzie moment,że podswiadomość sie odpali i po ptokach;)) |
|
To ja chyba już w małym stopniu jestem "człowiekiem" >;P Bo jak czuje emocje to się zastanawiam nad.... celem >;))
|
Wiesz,to akurat jest bardzo na plus,mało kto tak potrafi. Trzeba dużo pracy nad sobą,ja pracuję ze soba aby zminimalizować emocje bo emocje prowadzą na manowce. Co innego mieć uczucia a co innego odpalić sobie agresję ,strach itd. |
|
To spróbuj wywoływać emocje na życzenie to z NLP a potem można hmm zagrać "melodie" na swoim umyśle to dopiero mało kto umie >;) radość, smutek, wstręt, strach, zaskoczenie i złość >;P

|
|
|
Re: Szykuje się, poważna rozmowa? >;))
|
Zabanowany
|
Ten post był aktualizowany .
ZAWARTOŚCI USUNIĘTE
Autor usunął wiadomość.
|
«
Wróć do Magiczna Kawiarenka
|
1 przeglądaj|%1 wyświetleń
| Free forum by Nabble | Edit this page |

