Konstrukcja 2.
Konstrukcja 2
Ptolemeusz w swoim dziele Almagest[2][3] opisuje sposób znalezienia długości boku pięciokąta wpisanego w zadany okrąg.
Narysuj okrąg o środku S.
Narysuj średnicę okręgu i prostopadły do niej promień BS.
Znajdź środek A jednego z promieni zawierających się w średnicy.
Narysuj łuk o środku A i promieniu AB, punkt jego przecięcia ze średnicą oznacz C.
Odcinek BC ma długość boku pięciokąta wpisanego w wyjściowy okrąg.
Konstrukcja 3.
Konstrukcja 3
Metodę Ptolemeusza można rozbudować, uzyskując algorytm znalezienia wszystkich pięciu wierzchołków na okręgu.
Narysuj okrąg o środku S.
Narysuj prostą przechodzącą przez S i przecinającą okrąg w punktach A i B.
Narysuj promień CS prostopadły do średnicy AB.
Znajdź środek odcinka BS i oznacz go D.
Narysuj łuk o środku D i promieniu CD, punkty jego przecięcia z prostą AB oznacz E i F.
Narysuj łuk o środku C i promieniu CE, punkty jego przecięcia z okręgiem oznacz G i H.
Narysuj łuk o środku C i promieniu CF, punkty jego przecięcia z okręgiem oznacz I i J.
Punkty C, G, H, I, J są wierzchołkami pięciokąta foremnego.
Konstrukcja 4.
Konstrukcja 4
W poniższej konstrukcji wykorzystano okrąg Carlyle’a[2].
Narysuj okrąg o środku O.
Przez punkt O poprowadź prostą k, punkty jej przecięcia z okręgiem oznacz Q i P.
Narysuj promień OA prostopadły do średnicy QP.
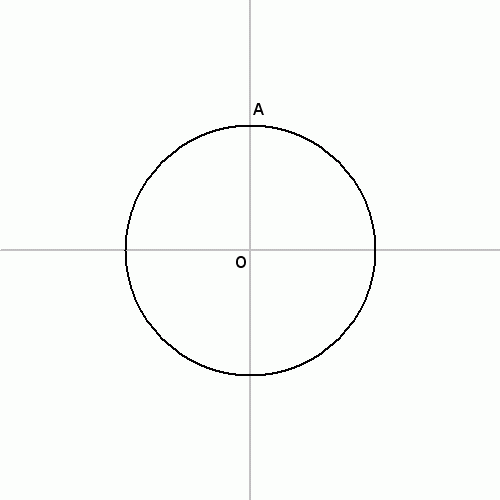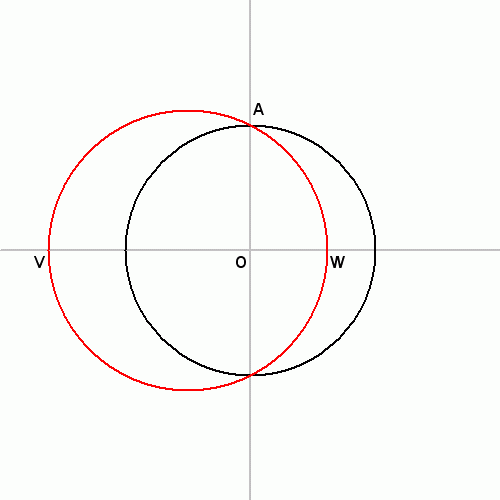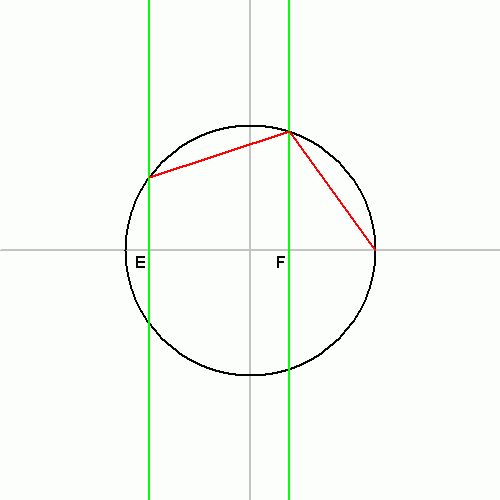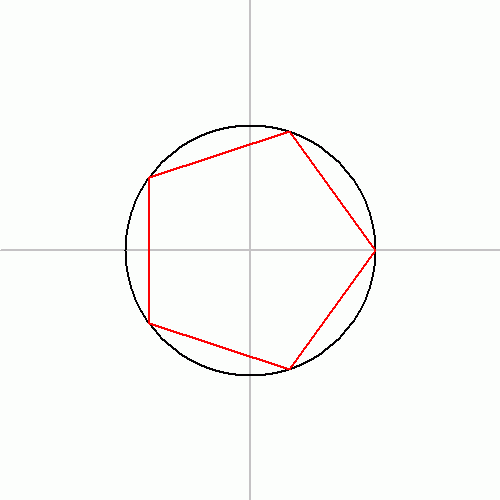
Znajdź środek M promienia OQ.
Narysuj okrąg o środku M przechodzący przez A; punkty jego przecięcia z prostą k oznacz V i W.
Zakreśl łuk o środku W i promieniu OP, punkty jego przecięcia z wyjściowym okręgiem oznacz P1 i P4.
Zakreśl łuk o środku V i promieniu OP, punkty jego przecięcia z wyjściowym okręgiem oznacz P2 i P3.
Punkty P, P1, P2, P3, P4 są wierzchołkami pięciokąta foremnego.