Lothar. napisał/a
Dogoniłem w dojrzewaniu, a potem, to..... potem >;P Mam swoją hipotezę, zawierającą to że owa przeszkoda okazała się.... opłacalna >;) Więc "leczenie" statystycznie sprowadzi "straty", może zostawić jak jest?
Rozkład normalny, rozkład Gaussa[2] (w literaturze francuskiej zwany rozkładem Laplace’a-Gaussa) – jeden z najważniejszych rozkładów prawdopodobieństwa, odgrywający ważną rolę w statystyce. Wykres funkcji prawdopodobieństwa tego rozkładu jest krzywą w kształcie dzwonu (tak zwaną krzywą dzwonową).
Przyczyną jego znaczenia jest częstość występowania w naturze. Jeśli jakaś wielkość jest sumą lub średnią bardzo wielu drobnych losowych czynników, to niezależnie od rozkładu każdego z tych czynników jej rozkład będzie zbliżony do normalnego (centralne twierdzenie graniczne) – dlatego można go bardzo często zaobserwować w danych[a]. Ponadto rozkład normalny ma interesujące właściwości matematyczne, dzięki którym oparte na nim metody statystyczne są proste obliczeniowo[b].
Definicja rozkładu normalnego
Istnieje wiele równoważnych sposobów zdefiniowania rozkładu normalnego. Należą do nich: funkcja gęstości, dystrybuanta, momenty, kumulanty, funkcja charakterystyczna, funkcja tworząca momenty i funkcja tworząca kumulanty. Wszystkie kumulanty rozkładu normalnego wynoszą 0 oprócz pierwszych dwóch.
Zobacz w Wikiźródłach tablicę rozkładu normalnego
Funkcja gęstości
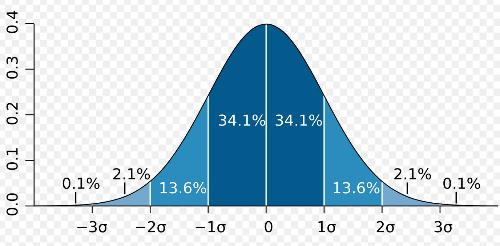
Ilustracja reguły trzech sigm
Zobacz też: funkcja wykładnicza i pi.
Funkcja gęstości prawdopodobieństwa rozkładu normalnego ze średnią μ \mu i odchyleniem standardowym σ (równoważnie: wariancją σ 2 \sigma ^{2}) jest przykładem funkcji Gaussa. Dana jest ona wzorem:
f μ , σ ( x ) = 1 σ 2 π exp ( − ( x − μ ) 2 2 σ 2 ) . {\displaystyle f_{\mu ,\sigma }(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\exp \left({\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}\right).}
Fakt, iż zmienna losowa X X ma rozkład normalny z wartością oczekiwaną μ \mu i wariancją σ 2 \sigma ^{2} zapisuje się często X ∼ N ( μ , σ 2 ) . {\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).}
Uwaga: W wielu źródłach rozkład normalny jest oznaczany przez N ( μ , σ ) . {\displaystyle {\mathcal {N}}(\mu ,\sigma ).}
Jeśli μ = 0 \mu =0 i σ = 1 , {\displaystyle \sigma =1,} to rozkład ten nazywa się standardowym rozkładem normalnym, jego funkcja gęstości opisana jest wzorem:
ϕ 0 , 1 ( x ) = ϕ ( x ) = 1 2 π exp ( − x 2 2 ) . {\displaystyle \phi _{0,1}(x)=\phi (x)={\frac {1}{\sqrt {2\pi }}}\,\exp \left(-{\frac {x^{2}}{2}}\right).}
We wszystkich rozkładach normalnych funkcja gęstości jest symetryczna względem wartości średniej rozkładu. W rozkładzie normalnym prawdopodobieństwo, że wartość zmiennej (cechy statystycznej) znajduje się w odległości nie większej (mniejszej) niż jedno odchylenie standardowe od średniej wynosi w przybliżeniu 68,3%. Prawdopodobieństwo to wynosi odpowiednio 95,5% i 99,7%, dla odległości dwóch i trzech odchyleń standardowych od średniej (reguła trzech sigm). Punkt przegięcia krzywej znajduje się w odległości jednego odchylenia standardowego od średniej.